Hans Z. Munthe-Kaas
 Photo: Melanie Burford
Photo: Melanie Burford
Contact Hans Munthe-Kaas:
Research
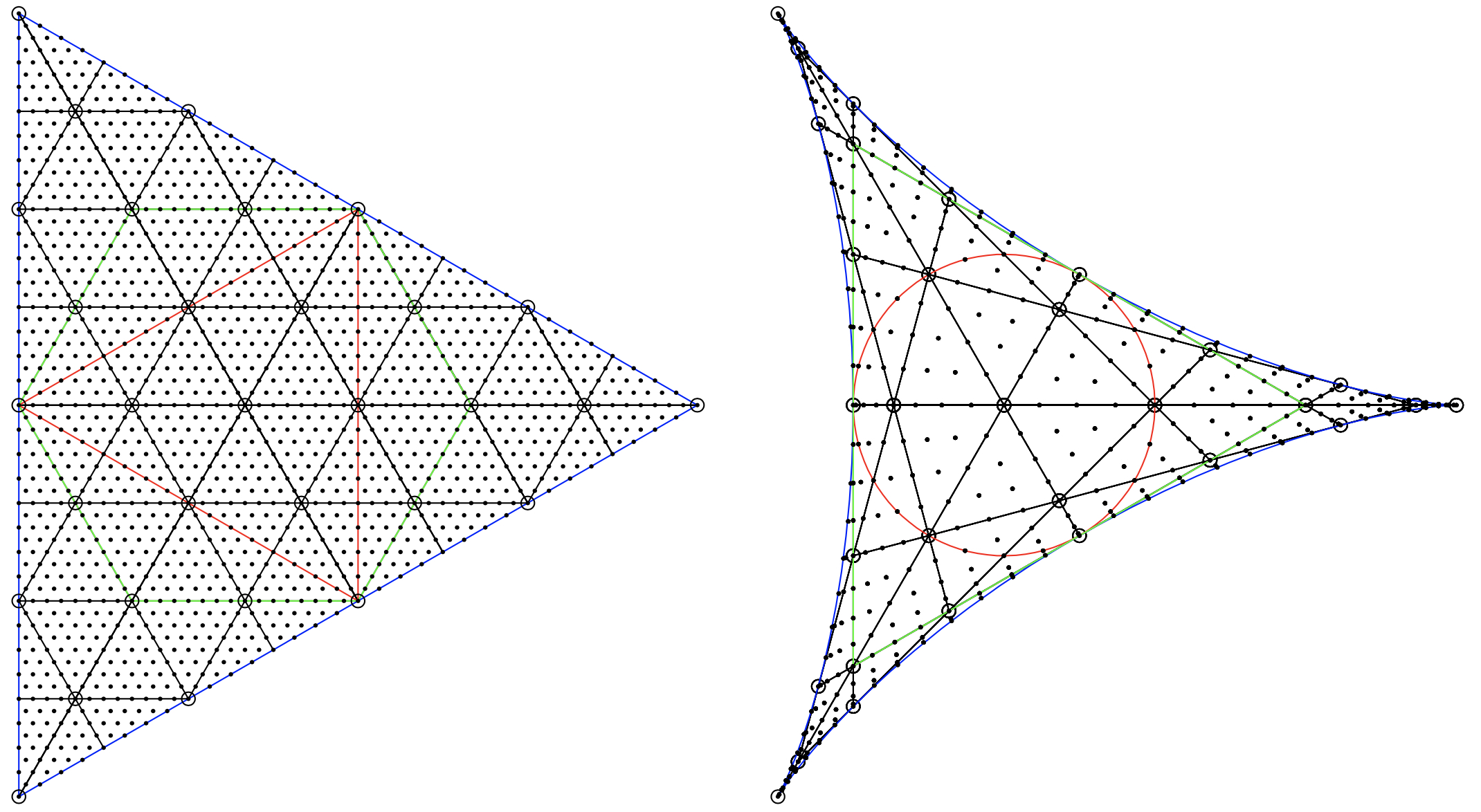 Multivariate Chebyshev polynomials. Domain of A2-family.
Multivariate Chebyshev polynomials. Domain of A2-family.
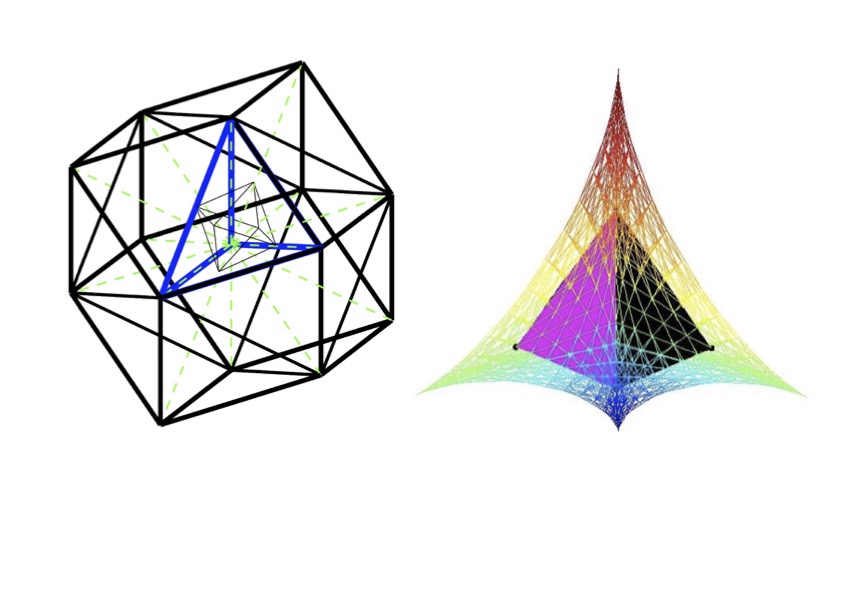 Multivariate Chebyshev polynomials. Domain of A3-family
Multivariate Chebyshev polynomials. Domain of A3-family
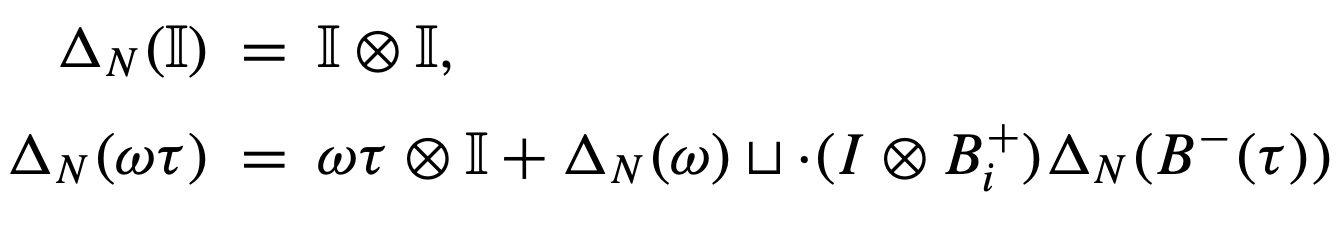 Coproduct of the MKW Hopf algebra
Coproduct of the MKW Hopf algebra
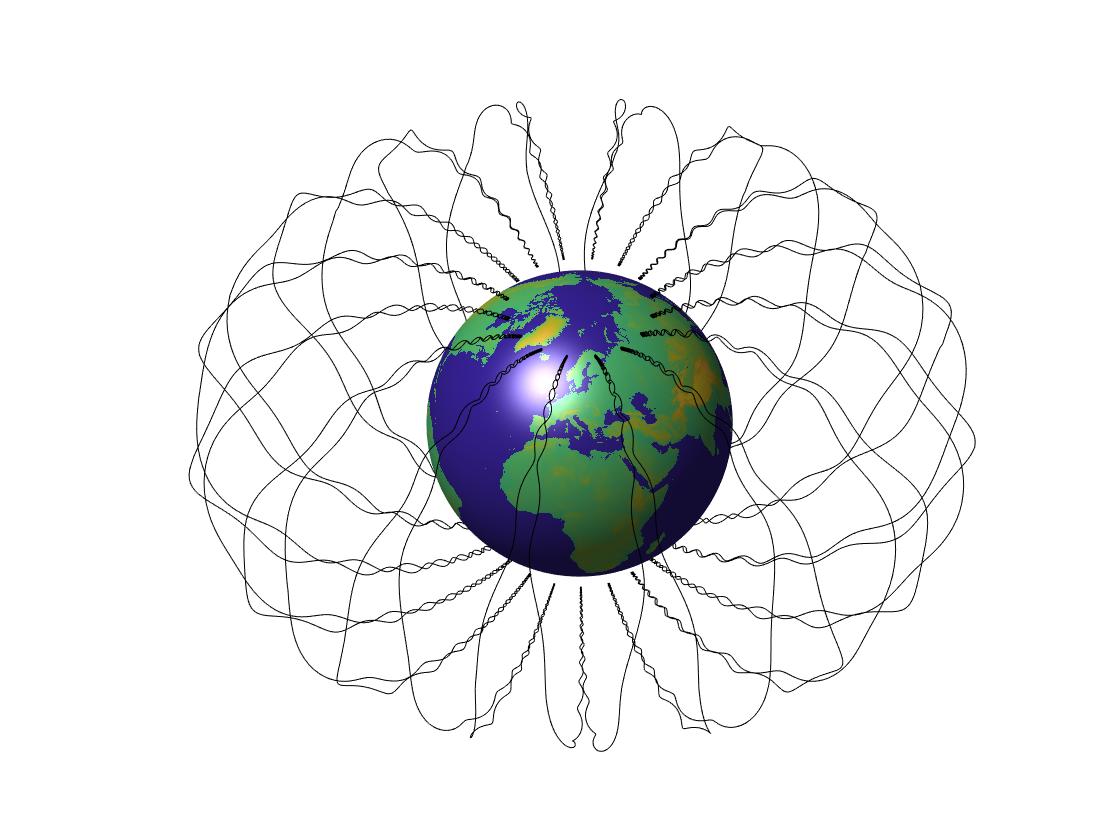 Lie group integration of Størmer's problem
Lie group integration of Størmer's problem
Research overview
Overview
My research is in the borderland between pure- and applied mathematics and computer science. A recurring theme is the role of mathematical abstractions in computational science, both as a tool for constructing efficient algorithms and as an organizing principle for computational software. Thus, as an overall label, most of my work is within Foundations of Computational Mathematics.
I am interested in applications of differential geometric techniques, geometric integration and structure preserving algorithms for solution of differential equations. Lie group integrators are numerical integration methods for differential equations built from coordinate independent operations such as Lie group actions on a manifold. Lie group integrators have been developed in tight cooperation between the research groups in Bergen, DAMTP Cambridge and mathematics NTNU.
Analysis of numerical Lie group integrators lead us to the study of new types of formal power series for flows on manifolds. Lie-Butcher theory combines classical B-series for integration schemes with Lie series. This research activity has connections to many areas of mathematical research such as control theory, stochastic differential equations, renormalization, combinatorial Hopf algebra theory and non-commutative symmetric functions.
In my PhD (1989) I, among other things, investigated FFTs for functions possessing crystallographic symmetries. After 2004, I have again found interest in this topic, due to connections between this theory and multivariate versions of Chebyshev polynomials. This is applied in the construction of spectral element methods based on triangular and simplicial subdivisions of the domain. A related topic is applications of Fourier transforms on groups, with applications in numerical linear algebra and image processing.
My PhD work, for which I was awarded the Esso prize in 1999, was on numerical linear algebra and parallel algorithms. I was interested in applications of group theory in the construction of fast elliptic solvers, as well as an organizing principle for massively parallel computations. In the early 1990s I was writing software and developing algorithms for massively parallel computers, in particular FFTs and various algebraic techniques for routing permutations on massively parallel computers. I was also interested in construction of permutation networks, in particular I studied some generalized shuffle-exchange networks. These are based on interesting connections between permutation networks and the theory of linear shift registers.
Object oriented program design is founded on the distinction between specification and implementation, or ‘what’ and ‘how’. This is a well established principle in core computer science. In computational mathematics, however, software has traditionally been organized around coordinate based formulations and discrete representations. In the SOPHUS project, initiated around 1991, we investigated coordinate free formulations for numerical algorithm design and for numerical software. In particular we developed coordinate free formulations of tensor computations and this was also an initial motivation for the study of Lie group integrators. The DiffMan Matlab toolbox for solving differential equations on manifolds is based on the ideas of the SOPHUS C++ library.
Teaching
 Teaching ‘Mattesirkelen’ for high school students
Teaching ‘Mattesirkelen’ for high school students
Munthe-Kaas has over more than three decades been lecturing courses in applied mathematcs, pure mathematics, and computer science at all university levels, from advanced seminars to introductory courses. Internationally he has given advanced courses at AIMS South Africa, at a CIMPA school in Brazil, at Morningside Centre in Beijng, Uppsala University Sweden, and he has given lecture series various research semesters.
Teaching autumn 2021: Mat101 (precalculus).
Students who want master thesis projects: Please take contact.
Outreach

Lorem ipsum dolor sit amet, consectetur et adipiscing elit. Praesent eleifend dignissim arcu, at eleifend sapien imperdiet ac. Aliquam erat volutpat. Praesent urna nisi, fringila lorem et vehicula lacinia quam. Integer sollicitudin mauris nec lorem luctus ultrices. Aliquam libero et malesuada fames ac ante ipsum primis in faucibus. Cras viverra ligula sit amet ex mollis mattis lorem ipsum dolor sit amet.
Lorem ipsum dolor sit amet, consectetur et adipiscing elit. Praesent eleifend dignissim arcu, at eleifend sapien imperdiet ac. Aliquam erat volutpat. Praesent urna nisi, fringila lorem et vehicula lacinia quam. Integer sollicitudin mauris nec lorem luctus ultrices. Aliquam libero et malesuada fames ac ante ipsum primis in faucibus. Cras viverra ligula sit amet ex mollis mattis lorem ipsum dolor sit amet.
Lorem ipsum dolor sit amet, consectetur et adipiscing elit. Praesent eleifend dignissim arcu, at eleifend sapien imperdiet ac. Aliquam erat volutpat. Praesent urna nisi, fringila lorem et vehicula lacinia quam. Integer sollicitudin mauris nec lorem luctus ultrices. Aliquam libero et malesuada fames ac ante ipsum primis in faucibus. Cras viverra ligula sit amet ex mollis mattis lorem ipsum dolor sit amet.
Lorem ipsum dolor sit amet, consectetur et adipiscing elit. Praesent eleifend dignissim arcu, at eleifend sapien imperdiet ac. Aliquam erat volutpat. Praesent urna nisi, fringila lorem et vehicula lacinia quam. Integer sollicitudin mauris nec lorem luctus ultrices. Aliquam libero et malesuada fames ac ante ipsum primis in faucibus. Cras viverra ligula sit amet ex mollis mattis lorem ipsum dolor sit amet.
Lorem ipsum dolor sit amet, consectetur et adipiscing elit. Praesent eleifend dignissim arcu, at eleifend sapien imperdiet ac. Aliquam erat volutpat. Praesent urna nisi, fringila lorem et vehicula lacinia quam. Integer sollicitudin mauris nec lorem luctus ultrices. Aliquam libero et malesuada fames ac ante ipsum primis in faucibus. Cras viverra ligula sit amet ex mollis mattis lorem ipsum dolor sit amet.
Lorem ipsum dolor sit amet, consectetur et adipiscing elit. Praesent eleifend dignissim arcu, at eleifend sapien imperdiet ac. Aliquam erat volutpat. Praesent urna nisi, fringila lorem et vehicula lacinia quam. Integer sollicitudin mauris nec lorem luctus ultrices. Aliquam libero et malesuada fames ac ante ipsum primis in faucibus. Cras viverra ligula sit amet ex mollis mattis lorem ipsum dolor sit amet.
Lorem ipsum dolor sit amet, consectetur et adipiscing elit. Praesent eleifend dignissim arcu, at eleifend sapien imperdiet ac. Aliquam erat volutpat. Praesent urna nisi, fringila lorem et vehicula lacinia quam. Integer sollicitudin mauris nec lorem luctus ultrices. Aliquam libero et malesuada fames ac ante ipsum primis in faucibus. Cras viverra ligula sit amet ex mollis mattis lorem ipsum dolor sit amet.
Elements
Text
This is bold and this is strong. This is italic and this is emphasized.
This is superscript text and this is subscript text.
This is underlined and this is code: for (;;) { ... }. Finally, this is a link.
Heading Level 2
Heading Level 3
Heading Level 4
Heading Level 5
Heading Level 6
Blockquote
Fringilla nisl. Donec accumsan interdum nisi, quis tincidunt felis sagittis eget tempus euismod. Vestibulum ante ipsum primis in faucibus vestibulum. Blandit adipiscing eu felis iaculis volutpat ac adipiscing accumsan faucibus. Vestibulum ante ipsum primis in faucibus lorem ipsum dolor sit amet nullam adipiscing eu felis.
Preformatted
i = 0;
while (!deck.isInOrder()) {
print 'Iteration ' + i;
deck.shuffle();
i++;
}
print 'It took ' + i + ' iterations to sort the deck.';
Lists
Unordered
- Dolor pulvinar etiam.
- Sagittis adipiscing.
- Felis enim feugiat.
Alternate
- Dolor pulvinar etiam.
- Sagittis adipiscing.
- Felis enim feugiat.
Ordered
- Dolor pulvinar etiam.
- Etiam vel felis viverra.
- Felis enim feugiat.
- Dolor pulvinar etiam.
- Etiam vel felis lorem.
- Felis enim et feugiat.
Icons
Actions
Table
Default
| Name |
Description |
Price |
| Item One |
Ante turpis integer aliquet porttitor. |
29.99 |
| Item Two |
Vis ac commodo adipiscing arcu aliquet. |
19.99 |
| Item Three |
Morbi faucibus arcu accumsan lorem. |
29.99 |
| Item Four |
Vitae integer tempus condimentum. |
19.99 |
| Item Five |
Ante turpis integer aliquet porttitor. |
29.99 |
|
100.00 |
Alternate
| Name |
Description |
Price |
| Item One |
Ante turpis integer aliquet porttitor. |
29.99 |
| Item Two |
Vis ac commodo adipiscing arcu aliquet. |
19.99 |
| Item Three |
Morbi faucibus arcu accumsan lorem. |
29.99 |
| Item Four |
Vitae integer tempus condimentum. |
19.99 |
| Item Five |
Ante turpis integer aliquet porttitor. |
29.99 |
|
100.00 |
Publications
Reverse chronologic order:
|
[1]
|
Hans Z Munthe-Kaas, Ari Stern, and Olivier Verdier.
Invariant connections, Lie algebra actions, and foundations of
numerical integration on manifolds.
SIAM Journal on Applied Algebra and Geometry, 4(1):49-68,
2020.
[ bib |
.pdf ]
|
|
[2]
|
Charles Curry, Kurusch Ebrahimi-Fard, Dominique Manchon, and Hans Z
Munthe-Kaas.
Planarly branched rough paths and rough differential equations on
homogeneous spaces.
Journal of Differential Equations, 269(11):9740-9782, 2020.
[ bib |
.pdf ]
|
|
[3]
|
Hans Z Munthe-Kaas and Alexander Lundervold.
Correction to: On post-Lie algebras, Lie-Butcher series and
moving frames.
Foundations of Computational Mathematics, 19(1):241-241, 2019.
[ bib |
.pdf ]
|
|
[4]
|
Gunnar Fløystad, Dominique Manchon, and Hans Z Munthe-Kaas.
The universal pre-lie-rinehart algebras of aromatic trees.
In International conference on Geometric and Harmonic Analysis
on homogeneous spaces and Applications in Honor of Professor Takaaki Nomura,
pages 137-159. Springer, 2019.
[ bib |
.pdf ]
|
|
[5]
|
Hans Z Munthe-Kaas and Kristoffer K Føllesdal.
Lie-butcher series, geometry, algebra and computation.
In Discrete Mechanics, Geometric Integration and Lie-Butcher
Series, pages 71-113. Springer, 2018.
[ bib |
.pdf ]
|
|
[6]
|
E. Celledoni, G. Di Nunno, K. Ebrahimi-Fard, and H.Z. Munthe-Kaas, editors.
Computation and Combinatorics in Dynamics, Stochastics and
Control.
Abel Symposia. Springer, 2018.
[ bib |
.pdf ]
|
|
[7]
|
Kurusch Ebrahimi-Fard, Igor Mencattini, and Hans Munthe-Kaas.
Post-Lie algebras and factorization theorems.
Journal of Geometry and Physics, 119:19-33, 2017.
[ bib |
.pdf ]
|
|
[8]
|
Robert I McLachlan, Klas Modin, Hans Munthe-Kaas, and Oliver Verdier.
Butcher series - A story of rooted trees and numerical methods
for evolution equations.
Asia Pacific Mathematics Newsletter, 7(1):1-11, 2017.
[ bib |
.pdf ]
|
|
[9]
|
Charles Curry, Kurusch Ebrahimi-Fard, and Hans Munthe-Kaas.
What is a post-Lie algebra and why is it useful in geometric
integration.
In European Conference on Numerical Mathematics and Advanced
Applications, pages 429-437. Springer, 2017.
[ bib |
.pdf ]
|
|
[10]
|
Hans Z Munthe-Kaas.
Groups and symmetries in numerical linear algebra.
In Exploiting Hidden Structure in Matrix Computations:
Algorithms and Applications, pages 319-406. Springer, 2016.
[ bib |
.pdf ]
|
|
[11]
|
Hans Munthe-Kaas and Olivier Verdier.
Aromatic Butcher series.
Foundations of Computational Mathematics, 16(1):183-215, 2016.
[ bib |
.pdf ]
|
|
[12]
|
Robert I McLachlan, Klas Modin, Hans Munthe-Kaas, and Olivier Verdier.
B-series methods are exactly the affine equivariant methods.
Numerische Mathematik, 133(3):599-622, 2016.
[ bib |
.pdf ]
|
|
[13]
|
Hans Munthe-Kaas and Olivier Verdier.
Integrators on homogeneous spaces: isotropy choice and connections.
Foundations of Computational Mathematics, 16(4):899-939, 2016.
[ bib |
.pdf ]
|
|
[14]
|
Gunnar Fløystad and Hans Munthe-Kaas.
Pre-and post-lie algebras: The algebro-geometric view.
In The Abel Symposium, pages 321-367. Springer, 2016.
[ bib |
.pdf ]
|
|
[15]
|
Kurusch Ebrahimi-Fard, Alexander Lundervold, and Hans Z Munthe-Kaas.
On the lie enveloping algebra of a post-lie algebra.
Journal of Lie Theory, 25(4):1139-1165, 2015.
[ bib |
http ]
|
|
[16]
|
Alexander Lundervold and Hans Z Munthe-Kaas.
On algebraic structures of numerical integration on vector spaces and
manifolds.
Faà di Bruno Hopf Algebras, Dyson-Schwinger Equations, and
Lie-Butcher Series, pages 219-263, 2015.
[ bib |
http ]
|
|
[17]
|
Kurusch Ebrahimi-Fard, Alexander Lundervold, Igor Mencattini, Hans Z
Munthe-Kaas, et al.
Post-Lie algebras and isospectral flows.
SIGMA. Symmetry, Integrability and Geometry: Methods and
Applications, 11:093, 2015.
[ bib |
.pdf ]
|
|
[18]
|
Hans Z Munthe-Kaas, Gilles Reinout W Quispel, and Antonella Zanna.
Symmetric spaces and Lie triple systems in numerical analysis of
differential equations.
BIT Numerical Mathematics, 54(1):257-282, 2014.
[ bib |
.pdf ]
|
Earlier publications
This file was generated by
bibtex2html 1.96.
 Photo: Melanie Burford
Photo: Melanie Burford


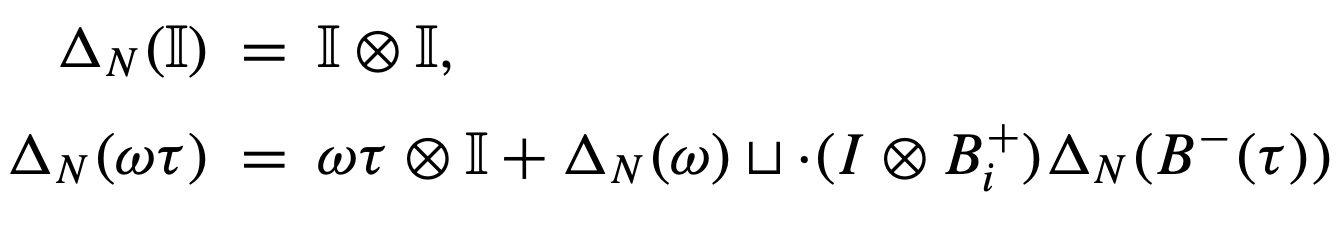 Coproduct of the
Coproduct of the 
 Teaching ‘Mattesirkelen’ for high school students
Teaching ‘Mattesirkelen’ for high school students